Relativity of Simultaneity in Distributed Computing
Contents
About a year ago, I described an allusion to physical phenomena in computing in "Caching and Levers". This post is devoted to a more complex theory, namely the Special Theory of Relativity (STR), and mostly to one of its implications, the "relativity of simultaneity".
Relativity of Simultaneity
Special Theory of Relativity may be approached as a set of equations for coordinate translation that take their effect as the speeds of objects approach the speed of light, c.
STR is based on two postulates, one of which states that light is always propagated in empty space with a constant velocity c regardless of the speed of the emitting body. This may be used to introduce a tricky paradox.
Train car experiment
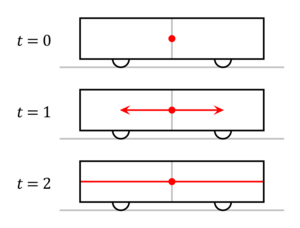
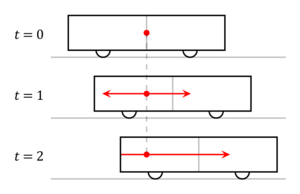
As seen by a passenger of the train. The events happen simultaneously.
As seen by a spectator on the station. The "back" event happens earlier than the "front" event.
(pictures from Wikipedia)
Assume that a train car is passing you when you're standing on a station platform. The train car has a lamp installed exactly at its middle. When the train passes you, a lamp flashes, and then you watch when the light reaches the front and the back of the car. It's interesting that those who sit in the car will notice the light hitting the two walls simultaneously, while those who stand at a platform will notice the back wall lit earlier than the front one. This is implied by the postulate described above: as seen by a spectator on the platform, the light propagates with equal speed at all directions, so it will hit the rear wall before the front one, as the former moves toward the light source, while the latter reproaches it. See wikipedia for more info.
This paradox, known as relativity of simultaneity may be formulated more generically: whether several events are simultaneous, depends on the location one watches them.
But what does it have to do with the computing? Before I answer this, I'd like to share what I've learned from a CACM magazine.
Quiescent consistency
In the multicore age, the classical data structures we all know about are about to change. The reason for that is the increasing demand on computation speed and volume that careful "sequential" CPU chip engineering is no longer capable to provide.
This challenge makes us rethink our approach to algorithm and data structure design. If we want data strctures to be efficient, we no longer may expect them to behave as good old ones in the sequential edge.
In distributed programming, there is an approach to describe data structure behavior known as quiescent consistency. There is a number of consistency conditions, sequential consistency, linearizability and others. These conditions describe how an object behaves when there are several threads calling its methods.
A data structure possesses quiescent consistency if it is consistent between its states of quiescence, i.e. when there are no methods currently in progress. As soon as a quiescently consistent structure has no operations pending (i.e. reaches the quiescence), we may be sure that the executions of methods before this state and after this state is never interpositioned.
Imagine a quiescently consistent stack. An implementation of it is described in this CACM paper "Data Structures in the Multicore Age", the one where I first encountered the quiescent consistency concept. Assume the following sequence of events happen to the q.c. stack:
- Three pushes x,y,z
- Quiescence (the pushes are processed)
- Three more pushes a,b,c
- Quiescence (the pushes are processed)
- Three pops
- Quiescence (the pushes are processed)
- Three more pops
- Quiescence
Note that q.c. doesn't mean that a data structure guarantees nothing except for this specific consistency. Consistency condition only maps data structure behavior in a concurrent setting to a behavior in a single-threaded environment, i.e. it only limits the number of a multitude of different sequences of method calls that may happen for a specific set of multithreaded events. All the properties a data structure exhibit in this sequential processing should still apply.
Quiescent consistency guarantees that the first three pops return x, y, and z (in an arbitrary order), and the next three pops return a, b, and c, somehow intermixed as well.
Note that, unlike linearizability, quiescent consistency doesn't impose any ordering on results of pops if there was no quiescence between the initial pushes. For instance, if processing of the first and the third pushes do not overlap, the linearizability ensures the pops will respect this order, while q.c. (in case that the second push overlaps with both of them) doesn't ensure that.
Having noted that, q.c. looks like a very weak and useless property. However, it still implies correctness, which, however, is enough in many circumstances. Imagine that you need a pool of unique numbers. It is enough to use a q.c. counter; the numbers it returns will be unique, which should fulfill our initial purpose.
Do we really need stronger consistency?
However, the reasons why we may be satisfied with weaker consistency conditions are not constrained with the specific examples. Let's try to prove the opposite. Assume we're implementing a stack that is accessed from a number of threads. Quiescent consistency may be not enough because if a push of A precedes the push of B, then the pops should be ordered in the specific way, and quiescent consistency may not guarantee that.
But wait... We say, "If one push precedes the other," but do we really know what "precedes" mean? If two threads in our distributed computational system invoke push call independently, how can we be sure that one of them precedes the other? And is there any sense in defining a measure for that?
Let's reckon the paradox we described at the beginning. In one reference frame, one event precedes the other, and in a different reference frame it's vice versa. So whether one push happens before the other, depends on the place we look from, and is not—and may not be—determined by a central, ubiquitous authority. That's a law of the universe, and we can't change this in computing.
Surprisingly, it makes quiescent consistency be a fairly appropriate constraint for a distributed data structure. If there's no strict sense of precedence between events that happen in different places of our network then why can't we use this to develop a more efficient data structure? The correct answer is, "indeed, why not?", and such data structures are well-defined nowadays.
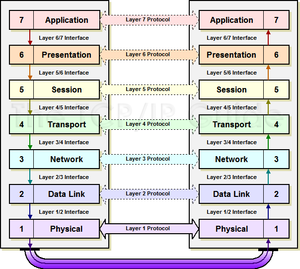
OSI model
OSI model is an abstraction that aims to make the design of distributed computation systems easier. The chain of events that happen during a process of data transmission is separated to several separated layers: each layer has its own protocol, which is independent of the actual implementation of the underlying layers. You may learn more at the wikipedia.
STR vs computing: the difference
We have successfully used a metaphor from physics in distributed computing, but there is an inherent limitation of applying the concept further. In physics, if we have a car of a specific length (as measured by its riders), we may install the light source in such a way that the events at two sides of it happen predictably simultaneous in the reference frame of the spectator at the station.
In computing, we can't do that. OSI model prevents us from predicting how fast the events happen by masking out the capabilities of a system at lower layers. In physical reality, we know that as soon as the light "hits" the back and front covers of the car, the event "happens" (or, more precisely, a piece of reflected light is launched towards the spectator). In computing, however, we don't even know how long it takes for a signal to reach another node. Moreover, the OSI model makes this impossible to predict. All the layers guarantee correctness, but do not have any timing conditions.
Conclusion
The absence of timing in the OSI model suggests that may be no sense in saying, "this structure may not be used, as it processed the request in the different order than they're issued in". The "order they're issued in" is inherently unpredictable in our computing models.
This inherent unpredictability of timings of processes and events, as described in OSI model, is why we really can't apply the special theory of relativity to computing. However, we still may notice that simultaneity in the world around us, as confirmed by physical experimentation, is relative. And the nature still works well!
And if the nature accepts it, why can't we learn from it, and allow our distributed systems to be less predictable, and trade this predictability for speed?..
And again, it appears that someone realized this before me.