Treap: simple balanced search tree
Contents
Balanced trees and programming contests
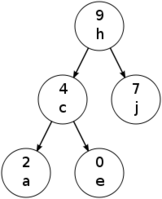
This is an example of treap: letters form an alphabetically-sorted search tree, while numbers are arranged as a heap.
Pic from Wikipedia

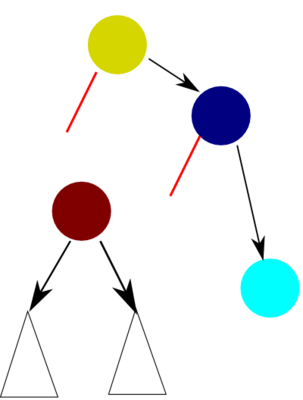
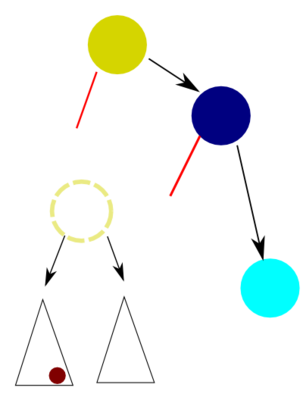
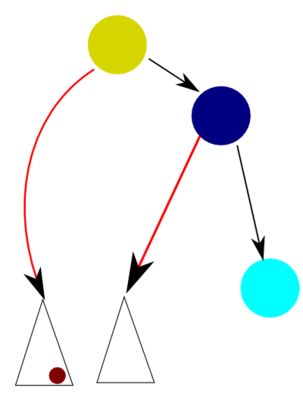
A balanced binary search tree is a binary search tree whose height is not big, around O(log N). This value is crucial, because search operation, the one these trees are named after, takes O(tree_height) time.
In a typical programming contest you're given 5 hours to write several programs, each of which, aside passing all jury's tests, meets specified time limit. One of keys to success is (or, at least, was) the ability to quickly code fast standard algorithms and data structures: disjoint sets, heaps, graphs, etc. And due to limited duration of competition not only should the algorithms be fast, but also easy to write in bug-free mode under an emotional pressure.
When it comes to the question how to implement a balanced binary search tree, most of programmers will outright shout "red-black tree!" (wiki). Indeed, it is balanced and is implemented in standard libraries of many languages, so it may seem a good choice (and even better as an advice) unless... Unless you're to code is yourself. It's implementation is way too complex, while the benefits of guaranteed indeterministic 2*log(N+1) height are sometimes not utilized.
A Treap in my mailbox
Back to the times when I was participating in those contests, I got a mail from one of our trainers. Within was a description of a nice data structure that I later discovered to be called treap. And now I'd like to tell about it.A treap is a conjunction of words "tree" and "heap" (or "tree" and "heap", for left-recursive readers). No wonder: it comprises properties of both tree and a heap. Or, more strict, it is a tree and a heap at the same time. Each node, aside from payload data, contains two keys; if we look at one key we will see a heap and if we look at another key we'll see a binary search tree.
Our main goal is nonetheless to build a balanced binary tree out of sequence of N key-value pairs that may come as an input in an unknown order. When you insert a node to a treap, you should pick up a uniformly distributed random number and use it as a heap-key. Of course, at the same time you should maintain search tree property for the tree-key.
Not as complex
Hell, the insertion procedure will be complex, you think. The trick is that restrictions usually help rather than prevent. So, assume we need to insert an element [Eh,Et] (that's heap and tree keys) to a (sub)tree with a given root [Rh,Rt].
- Eh < Rh - since we maintain heap, our new node should be added to one of the root's subtrees. To left or to right is decided based on tree-keys Rt <=> Et comparison, since we maintain tree as well. To insert element to a proper subtree we call the same insertion procedure recursively.
- Eh > Rh - our new node can only be a new root then (due to heap keys).
What will be its left and right subtrees? Let's assume that Et < Rt.
Then the right subtree of our new node will be the former root
(it can't be placed nowhere else due to heap-property), and the right
subtree of the old root will remain there.
Now, we're left with two dangling pointers (see picture B) and a subtree to split between them. But we can note that if we inserted the new node to that dangling subtree (picture C), it would be the root and its left and right children would fit the dangling pointers amazingly (picture D)! So to solve the original problem we need to solve it on a smaller tree... Smells recursive!
This leads to a tiny split procedure that, given a treap and a Kt tree-key, splits the treap into two treaps that can be left and right subtrees of a node with tree-key Kt in a binary search tree.
If you want to delete a node from tree, you'll need merge operation that makes one treap out of something that were left and right subtrees of a node we've just erased. This merge is the opposite to split and is as simple to implement. Red-black tree deletions require twice more code than insertions.
Implementation
The implementation of insertion stuff is here. Despite I haven't participated in contests for several years, I wrote it in 30 minutes from scratch (and benchmarking code took some additional time) and I didn't even have to debug the code. Can you repeat the same for a red-black tree insertions?
Unfortunately, it's hard to tie this small implementation into OOP concept, but in programming contests it was rarely needed.
If we run the script, we'll get fairly good height result on ascending sequence (on which unbalanced trees fail badly):
pavel@lonely ~/social/blog/treap $ perl -e 'for (1..10_000_000) { print "$_ ";} print "\n"' >test_file
pavel@lonely ~/social/blog/treap $ g++ --version | head -n 1
g++ (Gentoo 4.4.2 p1.0) 4.4.2
pavel@lonely ~/social/blog/treap $ g++ treap.cpp -O2 -o treap
pavel@lonely ~/social/blog/treap $ g++ treap.cpp -O2 -o tree_STL -DSTTREE
pavel@lonely ~/social/blog/treap $ time ./treap <test_file ; time ./treap <test_file ; time ./tree_STL <test_file
Height is 58 for RB it is 30.8499
real 0m6.545s
user 0m6.116s
sys 0m0.176s
Height is 56 for RB it is 30.8499
real 0m6.069s
user 0m5.908s
sys 0m0.160s
Height not supported :(
real 0m7.667s
user 0m7.472s
sys 0m0.188s
While height for RB-tree is about 30, height of a treap is about 50-60. You can run a series of experiments on your own and see it.
Why is it balanced?
The estimation of a height of a treap is O(log N).
The means, due to which the treap balances itself as a search tree, are Complex Math and are described in the articles linked at its Wikipedia page.
In common words, for a tree to be non-balanced not only search keys should be inserted in mostly ascending/descending order, but also the randomly generated numbers should also be arranged in the relevant order. This is unlikely. And if a heap_key is "out of sync" with unbalancing pattern, it rotates the subtree, for which it becomes a new root, so it becomes capable to absorb more "unbalancing" nodes without height increase.
Acknowledgements
Treaps were created by Cecilia R. Aragon and Raimund Seidel back in 1989.