"NP-complete!" as a lame excuse
Contents
Some time ago I bumped into a usual Stackoverflow question. A guy asked for a C# algorithm that could pick elements from array so that their sum is equal to a specified number. A usual NP-complete knapsack problem. But the answer made me think about an interesting matter. Let me screenshot the answer completely:
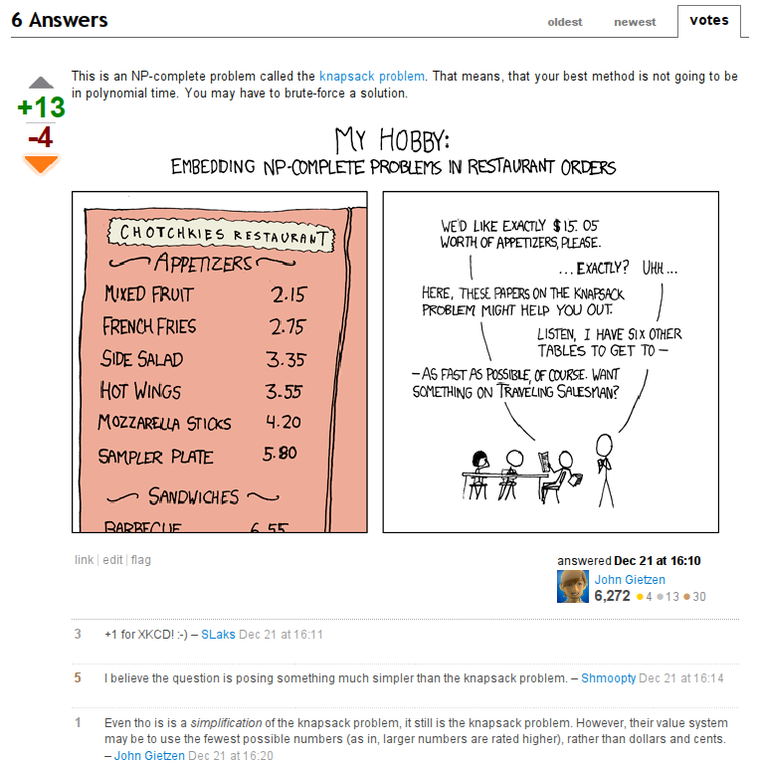
At a first glance, the answer contains everything an ideal answer should contain: a correct information, a certain bit of succinctness, and, a key to success, an XKCD comic. No wonder it was so highly upvoted.
However it was totally unhelpful.
Complexity classes
In Computer Science a concept of complexity class is used to define a class of problems, for which there exists an algorithm that runs on specified kind of abstract computing machine and uses specified amount of machine-specific resource. For example, famous NP class is defined as "set of problems that can be (a) solved on non-deterministic Turing machine (b) with use of polynomial number of steps with respect to the length of input". P class is the same but its abstract machine is a deterministic Turing one. The famous question of whether each NP problem is also P is still open.
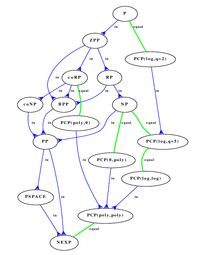
There is a lot of more tricky classes (PSPACE, for example, requires polynomial "memory"--maximal length of line of a Turing machine), which can even be parametrized (PCP(n,m) (probabilistically checkable proof), for example). The relationship between various classes is being studied, and aids the relevant research; here's a picture with some of them:
(pic from «Эффективные алгоритмы и сложность вычислений» book by Nikolai Kuzyurin and Stanislav Fomin (pdf, site; published under OPL license))
It clearly shows that the knowledge about complexity classes made its way into the minds of casual programmers. But instead of a challenge, it became a lame excuse.
What a casual programmer thinks when he encounters an NP-hard problem is, "Oh, it's NP-hard, so no known polynomial solution exists!". Some programmers even try to quickly make an algorithm that might solve something in specific cases, which they don't even realize. While what should be thought of is, "Oh, it's NP-hard, so no known polynomial solution exists! Let me derive constraints, and search for an approximate solution that fits it best!" Complexity theory statements and theorems should aid the solution, not substitute it!
Funny approximations for NP-hard problems
Honestly, I was among the programmers of the first type, as defined above. I used to being proud that I know that much of maths and was glad that I can blow the hopes of solving their problem. However a year ago I've taken an advanced complexity course (by guys from one of research groups in ISP RAS -- "group of Discrete Optimization Algorithms at Department of Mathematical Methods" (in Rus)) that actually revealed to me several amazing facts. Some complex NP-complete problems appear to have good approximations! Let me list several of them.
-
Edge-dominating set (wiki) -- assume we want to penetrate our adversary's network (which is an undirected graph). We should pick several channels (edges) to insert a virus into, and the hacking software will capture all information that passes through any of each channel's ends. We should cover the whole network with such "hacked" channels, so that each unhacked one is plugged into a node with a hacked channel. But at the same time, we should do it with minimum cost, i.e. minimum number of channels to hack. See figure A at the side for examples.
Figure A
Examples of edge-dominating sets from wiki page. Red edges are infiltrated channels. You may see that each non-hacked edge is touched by at least one hacked edge at joint router.
The task of picking such a minimum set is NP-hard. Brute-force? No, there is a better idea. We don't necessarily need minimum (although it would be nice), but instead we can hack some extra channels--the budget is not fixed anyway. We could use some clever algorithm to pick such edges, but instead... let's just hack arbitrary channels that aren't adjacent to already hacked ones!
What amazed me is that such a "solution"... will never exceed the real minimum number multiplied by two! "That's still too much", might the Greedy Manager have said, and he would be right. But the thing is that we even didn't try to solve anything: the dumbest algorithm yields a good, constant-factor approximation for a problem with yet unknown efficient exact solution. Hell, it's even easier to implement than a brute-force!
-
Knapsack problem (wiki) -- assume a burglar infiltrated a house. Unfortunately, he has a relatively small knapsack, into which he can't put everything of value. Possessing a discriminating eye, he can immediately determine how much the fence will pay for a thing. His aim is to maximize the cost of the stuff carried away, the overall weight being less than his knapsack may bear. But unfortunately he's also limited on time and has to do it quick.
Complexity theory proves that such task is NP-complete. So the burglar might pack every combination of items into his sack until he finds out the best. He would have been caught if he did that, because the owner would have returned by the time he completes the enumeration. So he chooses another solution. He uses a "greedy algorithm" and pick first a thing with best price/weight ratio, among those that still fit his sack.
A fool! He didn't know that it was the house of computer scientist, who knew that thieves are dumb and greedy, and who intentionally bought a piece of jewelery with best price/weight ratio in the house, but that piece doesn't allow any other thing to be put into the sack due to overweight. For arbitrary N, this trick can make the burglar take away N times less stuff than he could at most!
But a simple adjustment to its algorithm can be made to limit the possible loss to "at least 1/2 of maximum value". The burglar should do the same, but at the end compare the value of picked best price/weight items with the value of the most expensive item he can carry away. If it turns out to yield more profit take this thing and run away.
This is an example that a small hack can guarantee a good approximation.
- Longest path problem (wiki) -- assume we want to make our competitor lose money, and thus we try to delay shipment of a valuable package. We can make a janitor agent into the dispatcher's room, so he can see the map of the area (an undirected graph) and use the special phone to guide the courier by a longest path between source and destination (without cycles, of course, since the courier will suspect something and report it). He must do it quickly, but, unfortunately, picking such a longest path is an NP-hard problem.
We've seen approximations by constant factors before, but this task, unfortunately, can't have an approximating polynomial algorithm for each constant factor. Of course, that's true unless P = NP. But the fact is that its polynomial inapproximability by constant factor is proven unless P = NP. So we'll have to teach the janitor to yield worse approximations if we want him to succeed. And conclude that sometimes NP-hard problems just do not have simple hacks that solve them well.
There are more facts that concern randomized algorithms, which have a certain probability to hit a good solution; facts about more tricky, non-constant approximations, but they're far less fun and are more like boring math crunching, so I won't mention it here.
Conclusion
Albeit whether P=NP is still an open question, complexity theory contains many valuable achievements on solving everyday problems.
Do not make complexity theory just a source of lame excuses of not solving the problem or writing brute-force algorithms and garage-made heuristics that can guarantee noting. Some programmers call it all "clever cheats", but many hand-made "cheats" are of no help in approximations (as shown above with the first, most obvious "greedy" algorithm for the burglar). Instead of cheating, do not hesitate to perform a quick googling or consult experts in this area if you encounter an NP-complete/hard problem--a fast solutions with proven and limited weakness, and suitable for your specific task may exist, and may have been studied well.
Or, if you're curious enough, and possess certain bit of math education, you can study it on your own. English-speaking readers may check online pages of their favorite universities for book recommendations and, maybe, online lectures. I can't recommend anything in English since I haven't read such books. To a Russian-speaking reader I can recommend the book «Эффективные алгоритмы и сложность вычислений» by Nikolai Kuzyurin and Stanislav Fomin (pdf, site; published under OPL license), which we used during our studies at the university.
Comments imported from the old website
Well, such "answers" in some circumstances may be even useful. While some programmers just do not understand NP-related stuff, the others don't even know about it.
Thank you for "great website", btw. I've just hacked in, so if you re-login, I'll even see your name instead of mere openid link. :-)
I really liked the article, and very much agree with the point you are making. It is true that understanding what NP-completeness (or hardness) is is very important, but using that as an excuse for not even attempting to tackle the problem is a lousy solution.
As you rightfully mention, there are approximation algorithms (btw you could also check out http://www.cs.technion.ac.il/~reuven/ on that topic), and sometimes even the "bruteforce" solutions with their exponential complexity can perform suitably well - for example, when you know that the size of the actual data you'll be working on is small enough.
I could not agree more; I actually remembered that question at one point and thinking the same as you (unhelpful, useless response happily not understanding that NP-complete even means). For these reasons I really hate Stack Overflow some times, yet I am slightly addicted to it :)
Great website, by the way.