Parallel merge sort

We live in a loosely connected world. There's an increasing demand on middlemen, which connect different entities together.

This seemingly unrelated introduction is important for this post in two different ways:

• Parallelization of tasks to different processors also grows in demand, as it's like creating stuff that doesn't need middlemen;
• If there were not for social networks and forums, you probably would never know about interesting things created at the other end of the world.

So, back to the topic. I considered merge sorting as not parallelizeable well, with the same runtime estimate. However, several months ago, having disclosed this ungrounded opinion, a dweller of a message board of my university disproved it. That post linked an article, which describes an algorithm of a parallel merge sort, although is not the original source of it. It contains a brief, practical explanation, and I liked the algorithm so much, that I wanted to retell it here.

What concurrency we're interested in

Note that I'll describe not just a multithreaded version of the algorithm, challenge of which is a clever use of locking. The problem described here is to deploy merge sorting into the system with distributed memory.

All intensive calculations in this framework should be performed locally. However, each processor has a limited amount of on-site random-access memory. So the challenge is to split the processing into small chunks, which will be sorted and merged locally (complex calculations), and will be just flushed byte-by-byte to external memory at the beginning and at the end of processing.

Why merge sorting?

The thing is that merge sorting is actually an external sort. It means that it can handle amounts of data larger than size of RAM you have the random access to. This should make us think that it's parallelizeable, but it nevertheless doesn't directly lead to an obvious way to parallelize it.

The usual merge sorting looks like this, N being equal to 2:

1. Split the sequence to sort into N (nearly) equal chunks;
2. Sort each chunk (recursively);
3. Merge all chunks (at once of pair-by-pair). The challenge is to parallelize this step.

Each chunk out of these N could be processed individually and independently, and this is a huge achievement. But a challenge remains: how to parallelize the merging?

Parallelized merging: idea

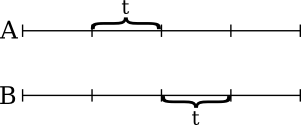
So, how to parallelize merging? First, we assume that one processor can store 2t cells in its own RAM, so we're restricted to merging only not greater than 2t cells at once.

Assume we have two large sorted arrays, A and B, which, merged, or even individually, don't fit into RAM available to one processor. This means that we should parallelize it: spit the sequence into small chunks that can be merged locally.

Let's try the obvious way: divide each array into chunks of length t and try to merge them sequentially. We can merge two first chunks into the beginning of the resultant array easily. But what if the elements of the 2^nd chunk should be merged inside the very same merged array?

This array of length of 2t already doesn't fit in the memory of one processor, so we cant merge it with the second chunk in the straightforward way.

So what we really want is to divide the arrays into mergable chunks. For example, what chunk in the corresponding B array should be A's sub-array (a_i,a_j) of length t merged with?

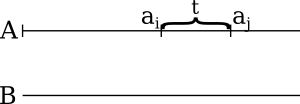
Obviously, the corresponding chunk (b_I,b_J) should be such that all bs with index less than k are less than a_i, and the similar holds for a_j.

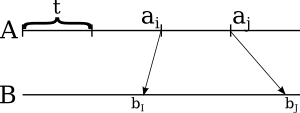
However, the size of (b_I,b_J) chunk could be greater than t, so we couldn't fit it into RAM to merge with the other chunk. Here, let's highlight some of the items that split B into chunks of length of t, that are inside the segment (b_I,b_J):

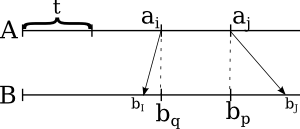
These new elements split B's chunk into smaller pieces, each of which is less than t. Let's find the corresponding elements in A array for them:

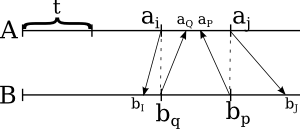
Now all chunks shown here have length less than t, and each corresponding pair could be merged.

But look what we've done here. The order, in which a_i, a_j, a_Q and a_P are arranged, is determined by merging them—or by merging [a_i,a_j] and [b_q,b_p] arrays. So if we merge these t-distant elements, we will determine the order of "splitters" that divide both arrays into mergable, ordered chunks.

Parallelized merging: the algorithm

The thoughts in the previous section lead to the merging algorithm. First, divide both arrays into (nearly) equal chunks of size t.

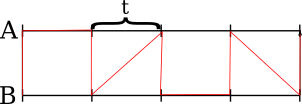
Then merge the two arrays that selected elements form. Use the same merging algorithm recursively. The result of this would be an order, in which the splitter elements should be arranged (marked with a red line):

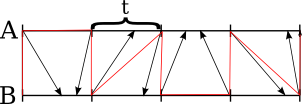
This performed merging allows us to determine the exact chunk of length t, into which should fit each splitting element from the other array, by simple calculations. (We should "switch" in what array we search for the counterpart at the same time as the red line switches sides.) Then you should use binary search to determine the actual place of it in the chunk, this way we'll generate twice more splitters for each array:

By construction, these arrows will not cross. Then, the pairs of chunks (the chunks to merge are depicted as sections colored in an alternating manner) will lay sequentially in the merged array. Merge each pair of chunks locally, and place the result into the larger array:

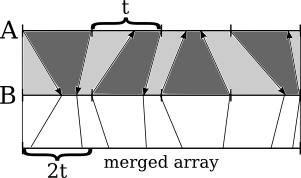
Each chunk to be merged consists of two segments of length less than t, which makes it possible to merge chunks locally on one processor. This completes the algorithm.

Parallelized merge: runtime estimation

Merging two arrays of n elements requires merging two arrays of n/t elements, performing n/t binary searches in arrays of length t, and, finally, merging the chunks we divided our arrays into, which takes O(N) operations. This leads to equation:

I'm too lazy to solve it, but T(n)=O(n) fits it (we consider t as a constant). This is the same estimate as in a usual merge, so parallel merge sorting is O(n⋅log n) as well.

You may note also note that parallel merge algorithm requires familiar pattern of divide-and-conquer iterations. And it's one of the neat facts about this algorithm: merging the chunks we sorted requires the very same processors that sorted the chunks!

***

This is an algorithm I was looking forward to talk about for a long time. I'm glad that I finally did this, and I hope that you didn't know it, and have spent the time learning new fun facts.