Performance metrics and parallelization
Contents
Some day you suddenly realize that a powerful PC is not cool anymore. Everyone works in clusters today! Clusters make our programs more fast, and if you goal is to fasten quite a long computation, they're of help.
Clusters of independent "computers" (in a broad sense) can scale differently: from several thousand tiny units on your GPU to thousands of different machines. And after you discover that you have a cluster available--or just several free PCs noone uses--you also meet the problem.
Programs suffer from insufficient attention paid to design them to run their parts concurrently. Probably, it's the right way to go, since the business value of early parallelization is not apparent. So the programs grow and their workflow ossifies. And when you finally find a parallelized medium to deploy the program onto, it's already too solid.
You have to cut your workflow to smaller pieces that may be computed independently. But where should you cut?
Performance metrics
To answer the question "how to break?" you must first answer "why?"
"To make my programs fast!" you answer, but speed may be understood differently! Here are two different "speeds", which one you pick?
The terms "throughput" and "response time" were adapted by me from different domains, and I'm not really sure that they're applicable here. If you know better terms for the concepts described, please, let me know!
- Given a lot of time, and having run the program a lot of times, maximize the number of fully completed tasks per time unit. I call this speed metric "throughput"
- Having run the program once, get final answer as fast as possible. I call this metric "response time"
Different tasks need different metrics. You should explicitly think about which one is the most suitable.
These metrics are very different, and hence they need different programs. Here's an extreme example. Assume you have N processors and your task can be divided into N independent sub-tasks of length t. Ideal distribution for response time looks like this:
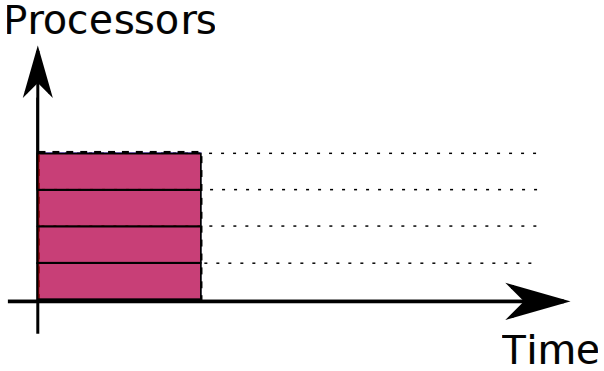
The time needed to complete the task is t, and you can't make it any less.
However, here's a not any less ideal task distribution for throughput:
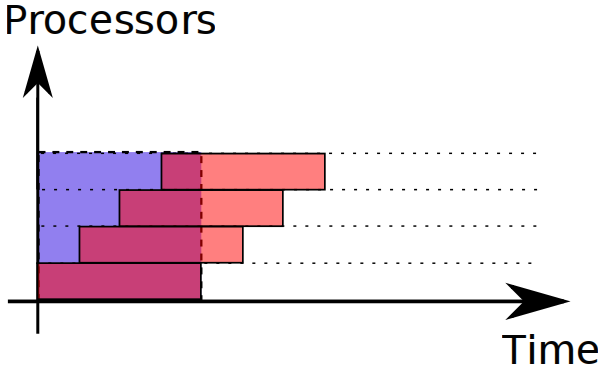
This distribution is not suitable for response time. Ideal distribution (shown by teal rectangle) yields response time nearly twice as fast.
However, for throughput it's not a problem, since we measure it for many runs of program. And for many runs this schedule is packed quite tight:
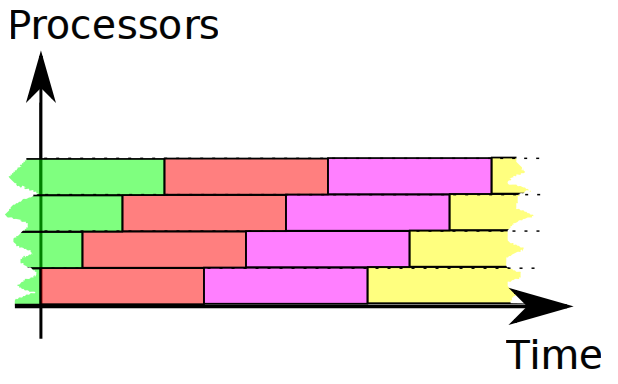
After we understood the difference, let's talk about response time metrics.
How to maximize response time
Each task of total length T has an unachievable ideal distribution across the N parallel machines. It was shown earlier by a teal rectangle; time it takes to get a response from such a computation is t = T/N. We can't make it in less time.
Assume that we created a task scheduling algorithm that completes in r time. The estimate of how bad our scheduling is could be estimated as (r - t)/t. We assume that our task has the first priority among others (i.e. the algorithm tries to finish it as soon as possible), and than the chunks are independent. These assumptions are not so uncommon, most systems that first compute a long list of independent tasks, and then execute it, fall into these assumptions.
Since the task is of first priority, then (r - t) < Δt, where Δt is the maximal length of the independent task (proof: if the inequality wasn't true, the last finished task should have been scheduled earlier). Here's the pic that demonstrates what we're talking about:
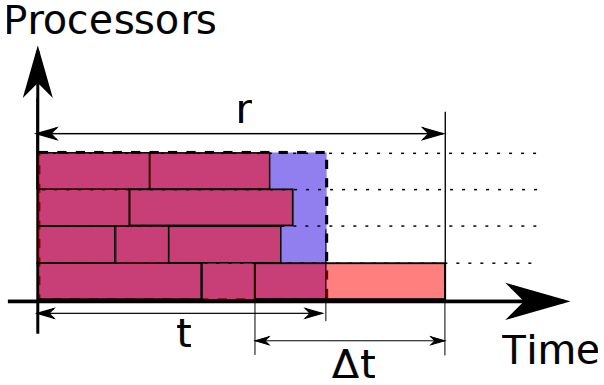
So, again, the badness of our algorithm is estimated as Δt/t; we're to minimize it. And there's just one straightforward way: to achieve the best response time, we should make independent tasks as small as necessary. We can stop dividing into chunks after we reach some acceptable badness (10%, for example); it's neither obligatory nor sensible to make the chunks as small as possible.
Conclusion
That's all I wanted to say. Perhaps it seems kinda obvious. But what shown here is the way to devise a good plan of action based on just setting a sane goal and doing small bit of maths (and maths do help in reasoning about real life). Actually, in the meeting I didn't draw formulæ, I just drew the pictures you see above--and we reached the agreement after that.
In further posts I'll pour upon the other performance metrics.
Comments imported from the old website
You asked for another word for "response time". Some people use "latency" to mean more or less the same thing.
"It's the Latency, Stupid" by Stuart Cheshire, May 1996.
Yeah, there's definitely something wrong with my post, and your comment makes me start to understand it... First thing is that I was very inaccurate with the terms I used, and this whole mess indeed looks unprofessional to me now. I'll rewrite my post in a couple of weeks, and I thank you for an inspiring comment!
Here's a "small" fix to this flaw.
First, Δt/t is not a property of scheduling. It's a property of partitioning of the whole work into chunks. It's therefore meaningless to say that "this schedule has better Δt/t than that schedule". However, this doesn't affect validity of your further reasoning.
It's true that, according to the metric, the first partitioning you describe should be "better" than the second. However, what does "better" mean? I didn't explain this in my post, while I should. A partitioning is "better" than the other if the maximum response time of all possible "sane" schedules is less that that of the other.
(A "sane" schedule is the one that doesn't make a processor stall in presence of tasks that haven't yet been started on any other processor.)
I.e. we can just implement a quick-and-dirty first-come-first-served algorithm for this NP-hard problem (and it's OK, since this component is not mission-critical). This metrics will make us assured that when we hit a "bad" case, it will be better when the partitioning is "better".
Moreover, the reason is not just in NP-hardness. In the problem we tried to solve the tasks:
- actually had some dependencies between them (not much, though);
- had unknown lengths; any task could just unpredictably terminate. However, the lengths had a common bound: "no task could be longer than
Δt".
I think that Δt/t provides quite a good, practical assessment of badness, and, most importantly, it guides us to making a better partitioning. The post was mainly about practice than about theoretical issues, actually. However, I failed to demonstrate the connection between these formulæ and practice, let alone to follow my own earlier advice to refrain from using home-made quick-and-dirty heuristics for NP-hard problems...
Thank you for the term "latency" (and the title of the article sounds like a harsh reminder :-D).
There seems to be a subtle flaw in your argument. I'm not sure if it affects your conclusion.
Let's call the last subtask to execute L.
Concrete example: Starting from the "old schedule" in the last image, make a "new schedule" by moving the short subtask to the left of L to the top processor, leaving a gap behind, and then slide L left into that gap. Let's also assume that new schedule makes L take a few percent longer time to execute.
The result is a new schedule that has slightly better response time, than the original schedule.
However, the "badness" approximation deltaT/T seems to indicate that this new schedule is worse than the original schedule.
And so picking the one of these two schedules that minimizes deltaT/T makes response time worse.
Generalize: Certainly chopping subtasks up into smaller subtasks -- as long as each task still does enough work that the per-subtask overhead is insignificant -- doesn't hurt response time. But if you don't change what gets assigned to the critical processor -- the processor that executes the L task -- then it is not possible to improve the response time, no matter how tiny you chop up the subtasks on the other N-1 processors.
Good Tetris players know some good heuristic solutions to this problem.