I wrote earlier that I know very few decent programming puzzles. To be more precise, I know one, The Prisoners Riddle. So I was reading that The Art of Multiprocessor Programming book (I already made a post influenced by what I read there, and I'll soon make another one--stay tuned). Some very interesting things the book tells about can be formulated as puzzles. Here's one.

Two threads need a mutex object with Lock and Unlock methods, but they only have three usual shared boolean variables. How to implement such a mutex?

Every thread can call GetThreadId() function which returns 0 for one thread and 1 to the other, and the boolean variables are automatically initialized to false before threads execute.

If you solved it, congratulations; you have just reinvented this wheel.

Since I know the solution, I can't really understand if it's a good riddle or not. It's definitely too hard for a job interview, but still, it can be a good one. So I need your comments. What do you think? Could you solve it?

As you already know, binary search is an O(log N) way to search if a particular value exists in a sorted array. There are some reports on how "most of our implementation" of binary searches are broken. The mistake discussed in that post is the overflow when calculating the index of the middle element. But regardless of whether you get this bit right, there's a different problem with all binary search implementations I've seen.

They're just too damn complicated and hard to get right out of your memory. Which is exactly what you want, say, at a job interview.

Recap

Let's recap what binary search algorithm is, at a high level. We are given a sorted array, and a value we're looking for. Is the value in the array? Here's the basic recursive algorithm:

1. Check if the middle element is the value? Yes--good, found it.
2. Is it smaller than what we're looking for? Yes--repeat the search in the array between the middle and the end of the original array.
3. So it must be larger then--repeat the search in the array between the beginning and the middle of the original array.

If you want a more detailed basic explanation, see other articles, e.g. this one. However, be mindful that many "simple" implementations make mistakes at the corner cases or present algorithms that require more special cases than needed. They might work for you but for me, they seem harder to remember. For example, the algorithm linked above has three if-else branches whereas we can do away with two. Read on how.

Key points

Almost always, if you're relying on your memory, you should prefer simple algorithms to complex, like you should implement a treap instead of an AVL tree. So here's a sequence of steps that helps me to write binary search correctly.

1. Simplicity: solve "bisection" rather than "binary search"
2. Consistency: use consistent definition of search bounds
3. Overflows: avoid overflows for integer operations
4. Termination: ensure termination

Let's explore them one by one.

1. Simplicity: Solve "Bisection" rather than "Binary Search"

From now on, let's redefine the problem. We aren't searching for anything anymore. "Searching" for an element in array is a bit hard to define. Say, what should "searching" return if the element doesn't exist, or there are several equal elements? That's a bit too confusing. Instead, let's bisect an array, pose a problem that always have a single solution no matter what.

Bisection is defined as follows: given a boolean function f, find the smallest k ≥ 0 such that, for all i < k, f(a[i]) == false, and for all j >= k, f(a[j] == true). In other words, we are to find the smallest k such that for all i within array bounds f(a[i]) == (i≥k). If the array is sorted in such a way that f(a[i]) is monotonic, being first false and then true, this problem always has a single solution. In some cases, when f(a[i]) is false for all array elements, the resultant k is greater by one than the last index of the array, but this is still not a special case because this is exactly the answer as defined by bold text above.

This is more powerful than the binary "search", which can be reduced to "bisection" as follows. In order to find if an element x exists in the array a of length N, we can do the following:

Now let's proceed with solving the bisection, now that we've defined it.

2. Consistency: use consistent definition of search bounds

Let's consider the array zero-indexed with length `N`, so the indexes range from `0` to `N-1`. The answer to our bisection problem is between `0` and `N` inclusively. Yes, `N` would be outside of the array bounds, but the answer to bisection can indeed be outside of the bounds if the entire array is smaller than the element we're searching for!)

We start by assigning i to 0, and j to N. No special cases allowed: we can do without them at all here. So at each step, we will check the value at index `k`, where i <= k < j. Inspecting this value will allow to reduce the range size.

3. Overflows: Avoid Overflows for Integer Operations

We literally have 1 integer operation here: given the bounds, compute the pivot point. i.e. the point at the middle of the array we'll apply f to to make a step. How hard can that be to compute the middle of an interval right?

Turns out, quite hard. This problem is discussed in the article I linked above more. If we lived in the world of unbounded integers, it would simply be (i+j)/2, but we live in the world of integer overflows. If i and j are positive integers, which makes sense for array indexes in C++, the never-overflowing expression would be:

Another useful property of this expression (in C++, at least) is that it's never equal to j if i < j. Here's why it's important.

4. Termination: ensure termination

A basic way to make sure that your program terminates some day is to construct such a "loop variant" that strictly decreases with each loop iteration, and which can't decrease forever. For our bisection, the natural variant is the length of the part of the original array we currently look for the answer in, which is max(j-i, 0). It can't decrease forever because its value would reach zero at some point, from which there's nowhere to proceed. We only need to prove that this variant decreases each iteration by at least one.

First step is to make sure that the time it reaches zero would be the last iteration of the loop (otherwise it wouldn't decrease!), so we use while (i < j).

Now assume that we've understood that the pivot point s does not satisfy the target function f. Our key difference with most binary search algorithms is that we should assign the new i to s+1 rather than s. Given our definition of the problem, s is never the answer in this case, and we should keep our candidate range as small as possible. If f(a[s]) is true, then s could still be the answer, so it does not apply here. Here's our iteration step now:

We mentioned in the previous section that i <= s < j, hence i < s + 1 and s < j, so each of assignments decreases j-i by at least 1 regardless of f's value. This proves that this loop never hangs up forever.

The complete program

So here's our bisection that works for all sorted arrays (in the sense of f(a[i]) being first false then true as i increases).

The search itself in terms of finding if a value exists in a sorted array, would be then written (I'm just repeating what I wrote above, no surprises here):

Proof By Authority

And GNU C++ STL implementation of binary_search follows the same guidelines I posted here. In my version of GCC 4.3.4 binary search looks like this:

Where lower_bound is the bisection function.

Conclusion

Here's my version of bisection and binary search I usually use when I need one. It is designed to be simple, and simple things are easier to get right. Just make sure your loop variant decreases, you do not overflow, and you get rid of as much special cases as possible.

Comments imported from the old website

It is hard to come up with a google-friendly name for the ||= construct you see in some programming languages quite often, "pipe-pipe-equals" being the is the closest (other names include "double-pipe equals," "or-equal," or "double-or equals"). Why should we name this monster in the first place? While cryptic at first sight, it is a very convenient shorthand that, I believe, allows us to write cleaner code. Let's see how it works on this example:

Essentially this ||= construct is equivalent to other convenience operators, such as +=. x += 2; means x = x + 2. The "or" operator || usually denotes a weak logical "or" that doesn't try to compute the left-hand side if the right-hand side is true. Usually, meaningful values evaluate to true, while the only evaluating to false are NULL pointers/empty values, zeroes, boolean Falses, and, sometimes, empty strings.

The statement is used mostly to set a variable to a "default" value if it's "unset" at some point. This gives the most visible advantage when you initialized dictionary elements in a loop. Here's a piece that saves counts of each array element into a dictionary (Ruby):

If you don't initialize output[x], you'll get a runtime error for trying to increment NULL. The advantage of ||= against other ways is that you don't repeat anything. You could have written the same piece as

But here you have to type output[x] twice and add two more lines of code, which is a complete waste of screen space and, possibly, computing resources if the interpreter doesn't optimize the duplicated computation out. Let's take a look how pipe-pipe-equals works in different languages (we've already seen it in action in Ruby).

Perl

Perl was the first interpreted language I learned, and the first place I saw the pipe-pipe-equals operator in. It works as expected, but is used less often than the direct version of the weak logical "or" to specify default parameters of a function. Here's how you'd put a default to a hash bucket:

This works in a strict mode, too. Note that, in Perl, many things evaluate to false, including empty strings (I once even tried to emulate it in Ruby). To restrict this action to undefs only, use //= in Perl6 instead, which sinks to its right like the Pisa tower, and look as if you're trying to put a division while drunk.

Python

Python has no equivalent of this operator. You have to type the very[long(expression)] twice, and it will be computed twice. You have several different ways to do this:

The engineers more experienced in Python programming, though, assure me that this is not a big deal since you have a different way of supplying default arguments for a function, which seemingly covers half of the use cases for pipe-pipe-equals (this doesn't prevent Ruby from having both, though). Another half is covered by dictionary's dict.get(key, []) method, so that the code piece #1 can be written in a succinct manner. But I still miss it.

Bash (Linux shell)

Bash? Its language is so simplistic, and it looks creepy; how come it would have an equivalent of such a beautiful shortcut? Here it is:

This assigns y to variable if the former is unset or null (as per Bash manual). I mostly used it to set default parameters for environment variables user may or may not set before invoking the script.

C++

While |= is a syntactically correct expression (C++ does not have the "short-circuit" version of this expression), it doesn't do what we discussed here.

C++ is statically typed, so the result of the standard logical "or" is boolean. Retaining the nice semantics we find in a dynamically typed language would require it to be "either the type of the left-hand side or the type of the right-hand side". This is hard to pull in a pass-by-value statically typed language.

Pass-by-value semantics also means that not everything can be assigned a NULL, and not everything can be converted to boolean value. C++ has default arguments as well as Python, so the same reasoning could apply here. You'll have to be more verbose in C++. That's probably why only |= expression is available, which is only useful if its left-hand-side is bool (see sidebar above for similar usage.)

OCaml

Everything said above about C++ applies to OCaml as well. Moreover, OCaml, as a functional language, doesn't have a flawless support for mutation, and pipe-pipe-equals statement its inherently mutational. However, its matching operator would require us to use the very_long_variable twice. However, OCaml and other functional languages have a very interesting construct called "option". If something has "X option" type, it may contain either "nothing" or a value of x. Then, this value may be "unpacked" trough pattern matching:

let very_long_variable = match very_long_variable with None -> y | Some t -> t

here, t is not an shorthand for another very long expression; instead, it's just an identifier, written as is. The match...with allows us to "unpack" values of structured (algebraic) types with shorthands like this. Since this was too long, OCaml has made this a library function Option#default:

let very_long_variable = Option.default very_long_variable y

Anyway, OCaml programs are even more explicit than those in C++ and Python, so trying to tie pipe-pipe-equals into them is quite pointless.

Ruby

"Erm, we saw how it is in Ruby at the beginning," you might think. Well, I lied to you a bit. The thing is that, in Ruby, it is not strictly equivalent to an assignment to a result of logical "or". Which do you think x ||= y is equivalent to?

In Ruby, and only for ||= and &&=, it's the second. If you assign to something other than a local variables, what looks like an assignment is actually a method call (think properties,) and, if so, this assignment does not happen at all if the left-hand side of ||= is false. Which makes sense, but looks like a special case. Read more here.

Why You Might not Need This

Some argue that this operator is mostly useless, especially if their favourite language doesn't have it. Here are some arguments they list.

Redundancy

Indeed, this expression is redundant. You can do the same in a multiple different ways, All the examples I demonstrated above showed how to write essentially a simple if statement in a very short-hand form. The number of characters spared is probably not worth it to include support for this feature to a language designer's must-have checklist.

The statement discussed decreases the redundancy in code in return of broader language definition; each language seeks a balance between these, and often leaves the pipe-pipe-equals aside.

Default Function Arguments

The ability to specify default function argument (C++, Python, Ruby, but not Bash or Perl) covers many use-cases for ||=. However, this doesn't help fancy loops that fill complex structures, one of which we showed above. Nor helps it when you have to specify the default parameter anyway but the concrete value is not known at the time of coding, and is an optional field user may or may not fill.

Confusion

It is confusing. The pipe-pipe-equals requires explanations how it works. It becomes a special snowflake, different from its "mathematical" counterparts +=, if a complex language wants to make its very useful (see Ruby section above). While "confusion" as an excuse of not doing something is my pet peeve (and I tried to explain why), it indeed requires some effort to understand the mechanics. I'm sure that you'll love it once you understand it, and the way I learned about this operator is not by reading a textbook or "The Most Confusing and Obscure Programming Language Features Possible" newsletter, but by reading someone's code.

To Use or Not To Use?

When it comes to deciding whether or not to use pipe-pipe-equals in the "creepy" way we discussed throughout the post, the criticism somehow fades out. If the language supports this, it will be used. I haven't encountered any coding style document that bans this feature. In Ruby and Perl, it is considered as good of an idiom as many. So the answer on the question of whether or not you sohuld use pipe-pipe-equals (||=) in your programs is, definitely, "yes".

If I was to explain Zeno's paradoxes to a layperson, I'd start with the Zeno's Flat Screen TV Paradox. It is very practical: most have firsthand experience in real-life application of this deeply philosophical problem each time we shop for something.

Imagine you come to a store, and see two TVs: a cheaper 30 inch one for $500, and a more expensive 50 inch one for $1000; otherwise the TVs are identical. Which one would you buy?

Zeno's Flat Screen TV paradox states that the only rational choice would be to buy a 50'' TV. Here's the proof.

Imagine you buy a 30'' TV instead. You bring it home, unpack it, start watching your favorite show, and a salesman knocks on your door. "Hey, I see your TV is only 30'' long," he says. "Would you like to upgrade to a 31'' TV for just 25 bucks?"

Well, 25 bucks isn't that much. It's like a half tank of gas, two cinema tickets, or a cab ride across the city. For that price, you permanently get one inch of screen diagonal! Only a fool wouldn't agree. You seal the deal, the salesman takes your old TV, and installs a new one, and you enjoy your 31 inch LED flat screen.

A moment later, a salesman knocks onto your door and asks if you'd like to increase a diagonal of your TV for 1 inch at only a $25 price. This is as good of a deal as the previous one, Even better: as the diagonal length increases, you get more screen space per inch for the same price! You seal the deal, and get a 32 inch TV. But before you even install it, a salesman knocks onto your door with a great offer...

This repeats until you end up paying $500 + 20*$25 = $1000 for a 50'' inch TV set--just as you could have done at the store in the first place. Since you got it as a series of increasingly lucrative deals, there is no sense to buy a 30'' one, and you should definitely go for a thousand dollar 50''. Which means that, a choice of a 30'' TV is never optimal.

Quot Erat Demonstrandum.

Note that it's sensible to manufacture smaller TVs in smaller quantities, because the comparison with a smaller screen is the gist of the paradox. Meanwhile, people have been buying 30'' televisions over and over, while this is completely irrational! And that's the Zeno's Flatscreen TV Paradox.

I remember this picture of my typical day two years ago. As sunny Russian winter morning finally banishes the dull winter night, I finally say "bye" to my girlfriend and leave for historical part of Moscow. Where I'm heading to, in a three-story, old cottage that predates even the communist government, lies my beloved office. I'm alone there. It is deserted, but not because of lay-offs, a party I'm not invited to, or because it's a one-man startup. It is just Sunday.

I log in to my workstation, and start doing it. Checking experiment results. Debugging new experiment frameworks. Just thinking, trying to push limitations of a suboptimal algorithm beyond what the humanty knows so far. Being productive, though less than usual: the presence of peers doing something pressures you to check reddit less frequently.

That was my typical Sunday afternoon two years ago. Today is Sunday too, and I'm writing this very sentence riding a ferry over the Bay rather than sitting in an empty office. To answer why, first I should understand why I went to the office on Sundays in the first place.

Integrity

Of course you've realized that the Sunday office was my shelter from the girlfriend, because it would be impossible to work at home in her presence. Keeping off of distractions is the reason why one would prefer to go to the office to do work, not just on Sunday, but on any other day. Other reasons exist, too.

One of them is psychological "anchoring". Office is associated in your mind as a place to do work, so your mere presence there, in formal clothing and in working hours, sets the right mood, and makes you more productive than relaxing in a comfy chair wearing slippers and a robe. The reverse is useful too: keeping work off of your home as much as possible makes your relaxation there more fulfilling.

Purely practical reasons kick in, too. At work, you have a fast intranet with a fast access to your cluster. It's somewhat amusing that at every place I worked as a programmer there was a cluster to which a large part of computation was offloaded. First it was a cluster that runs experiments, then it was a distributed software compiling and packaging system, and then the product itself was a distributed system that runs user's code. You definitely want to access this and other helpful corporate resources, such as repositories, with low latency.

Moreover, on your office machine you have a ready environment you work in, with editors opened, and consoles chdir-ed, so you can just dive in in and start instantly where you left. Finally, your corporate policies could prevent you from working from anywhere except the office for security reasons.

However, the reason why I no longer work on weekends is not that office became a less appalling place. The list above misses one crucial component.

Alone in the Ivory Tower

When I was a research intern, working on weekends was easy. I spent a lot of time coding new algorithms and experimenting with them, reading papers written by others, writing my own, or just thinking on stuff. I spent total of 2/3 of the overall time on these activities. They all have one thing in common: I could do this alone.

While interacting with others is a very important part of a researcher's work I used to underestimate, you could work alone for a good chunks of time and still be somewhat productive. No wonder I did. Besides, our project had only 4-5 people, and interacting with them just couldn't occupy much enough time.

Industry and a Larger Project

When I, as a Software Engineer, moved to what they usually call "Industry," I also tried to establish the stream of working on weekends. I managed to sneak in on two Sundays, but that was it. With a much more "officy" office, and still a challenging project, it didn't work anymore.

The work now demanded collaboration. The team was 5 times larger, and most of the work I was doing required to check with others frequently. Sometimes it was as ridiculous as making three meetings over three weeks to agree over a certain feature or change that took 15 minutes to implement. More often, you were just stuck waiting on others' decisions, on others' feedback, and on others' work as programmers or sysadmins.

I could find side projects and less important things a programmer always has in his backlog that required no collaboration, but unimportant work was never worth a Sunday spent in the office.

Besides, working on weekends now involved making peers feel uncomfortable. Some practical applications involved assigning a security guard to protect me working, which required me to apply for each weekend work permit separately as per company's policies. Application could be automated, but making another person waste his time was too much. I went twice, when the presence of the guard was justified by sysadmins and managers doing other work they couldn't postpone, and never bothered with it afterwards.

Let's Multiply By Ten

Although I spent weekends just like the normal people, I still stayed longer hours to get more work done. I still made security guards uncomfortable because they have much less opportunities to close earlier, but it was now legally my time anyway.

Now let's multiply by ten the size of the team, the volume of the codebase and the complexity of tasks, which describes my shift to the next job. The amount of work that could be done without the communication also shrunk by the same factor.

Email became the primary work tool. Most of the work is triggered either by notifications from others, then it is discussed with the peers who are much familiar with the codebase. When I am stuck with something I can spend hours in the late evening trying to debug the problem on my own, or I can ask my peers who worked on the project for a long time, and get it resolved within minutes.

Not only the office stopped to enjoy my visits on Sundays, I started to work late hours less. The communication with peers is no longer just red tape, it is the only way to be productive. And this communication is so much more efficient in the office than over e-mail, video conferencing, and phone calls, that you being in the office is inevitable. Studies showed ridiculously big numbers for how the bandwidth of the information our brain receives in real-world communication is larger than what we get by a video call. And it's more fulfilling, too.

To increase my productivity I even started watching my sleep cycle, and I now try hard to move my typical shift from 12-9pm to the normal 9-6pm. It doesn't work out well. I try.

Christmas as a Way to Enjoy an Empty Office

This amount of communication sometimes becomes overwhelming. The incoming mail speed starts to become more than the speed with which you can read it. No wonder that people started to value the Empty Office, when distractions and stress decrease, and you can just enjoy exercising your favorite art. Of special value is the US Christmas holiday, where you have two days others usually take an unpaid leave on so you can work with fewer interruptions.

Few come on weekends to achieve the same effect, of course, because it is still not productive; but a legitimate reason to have a less populated office is of understandable value.

***

I still like my job, and am as passionate about it as when I was younger; I still can handle 6-day work week. But, on Sunday, I'd rather read about something in the comfort of my home, go out with my friends, or visit some local nature. Hiking usually ends with a ferry ride with an awe-inspiring view on San Francisco skyline I can't really enjoy because—let's face it—I open my chromebook and read or write something about programming. I just don't do it in the office anymore.

This post is not about programming at all, but just about solving old problems with new computing tools. The old problem is finding the neighbourhood to rent the apartment in, and the tool is a map. Not just a map, but the Google Map. While looking at map when renting is a good advice, Google Map has a killer feature that unlocks a very new option.

Google Map can quickly recalculate the best public transportation route between two points on-the-fly while you drag one of them. This allows you to quickly learn what neighbourhoods provide a good commute to your specific office. You quickly uncover all possible commute options you have by moving the start marker around a neighborhood in order to filter then out the worst from your Craigslist search.

You may have other priorities rather than just getting the best commute, of course: quality schools, places to go out, parks nearby, et cetera.  I only describe how to filter by one criteria, and it doesn't have to be primary.

I only have four "small" requirements to daily commute:

• Public transportation. Driving a car in a big city is a nightmare, and commuting by bus or train allows you to read an interesting book or magazine (well, for now);
• Zero transfers. Each transfer drains your lifepower, and robs you of several minutes you could have been standing calmly, reading.
• Short total walk (5-10 minutes). Walking extra 10 minutes on a flat surface will have zero effect on your health, but will rob you of 10 minutes--or even more if you cross a lot of traffic lights.
• Overall time about 30 minutes. While you can do something while commuting, in-city public transport distracts you too much. 10 minute shorter commute saves you about 2.5 days per year, so investing 20 more minutes into commute time screening repays itself.

So for me, an ideal commute is a 30-minute ride on a bus or train directly to the office. And without Google Map I wouldn't know that I actually can accomplish this, and live in a cheaper neighbourhood at the same time. The map also uncovered a train stop I didn't pay much attention to--right next to the office.

So, here's a 6-minute video how to scan the area with a couple of tips of Google Maps usage.

(Here's a raw mkv if YouTube is banned in your country).

That was exactly how I scanned the city when I was looking for my new home. It turned out that I avoided the areas many people prefer to live in, but I found the best place specifically tuned for me instead.

Please, bear in mind that I know very little about the City of San Francisco, so I might have missed something, or discarded certain areas too vigorously. But knowledge may play against you: say, you know that you can arrive to Embarcadero by any train, and this prevents you from even trying to find closer public transport stops to your specific office, which Google Map does for you automatically.

There are more features in the Map I didn't show, and more ideas still implausible. You can set more preferences (click "More options," and select Bus/Train or prefer "Fewer Transfers"). You could use waypoint search if you were looking for a good commute for two persons at once (make a route between two offices, add a waypoint, which represents the home, and drag it over the map), but waypoints don't work for public transport for some reason, and this doesn't scale well for three, sadly. And if you know more tips, make your videos and comment here, I'd be happy to hear about them!

"Forget these silly runtime errors you had in Ruby: C++ is statically-typed!" Levap, a seasoned engineer, was enlightening the new hire. "You no longer have to wait while the sample run or unit tests finish to learn that your variables have the wrong type, nor you have to worry about this happening in production".

So, Paul, the younger engineer, stopped worrying. He went back to implementing a subclass that, unlike its parent, would only perform a low-level blocking write of data stored in a buffer object instead of more complex writing semantics found in the parent:

The new Write function would assert that the second parameter was false, and would just call a regular system's write, familiar to any C programmer. The only exception was that it fetched the target from the SimpleWriter object's private variables, and it wrote data chunk-by-chunk until finished. Hence, it didn't have to return the number of bytes written, and threw a fatal error on a severe error.

The yonger engineer soon found out that creating NeverBlockingWriter in place of SimpleWriter only required modifying method, and should involve no data copying. In a dynamic language, he would do just that by replacing the SimpleWrite method of the object with a nonblocking-only version, but in C++, Paul had to instantiate a whole new class and copy the information from the parent one to it. An alternative could be to force the superclass to be friends with its own child, which sounded more suitable for a dumb scene in a sitcom. Oh, if he only had the powers of Ruby...

Paul first merely called the parent's SimpleWrite(buffer, block), but then decided that calling SystemWrite directly was clearer and faster, so he fixed the code shortly afterwards:

This code looked right, but didn't work. What was worse, Paul planned to get the code working on the last hour before Christmas, and he couldn't, which created a sense of incompleteness and incompetence for the whole holiday.

What happened was that Paul updated the name of function to call, but forgot to update its arguments. Normally, C++ would barf a compile error in an instant. In this case, however, the trap was perfect: C++ silently, without a single warning, cast the pointer to Buffer to pointer to void, and boolean true to one. The program expected the other endpoint to reply to the data written, so the lack of the complete write created a very weird bug. Apparently, these functions were not different enough for C++ to show a compile error.

The fixed version immediately demonstrated that everything else was OK:

"Statically typed, my ass," were Paul's next words. Nobody heard him, since he stayed later to fight this bug.

Paul saved the code, and finally left the office. On his train, he shed a tear for OCaml that distinguished between integer and boolean, and promised that next time he saw a weird bug, he would check if he fell into another loophole in C++'s "static" typing.

"Lol, just pay more attention next time, smartass," the seasoned engineer advised.

Comments imported from the old website

A half a year ago, I've been challenged with improving functionality of a piece of software without making its interface more bloated than it already is. That made me thinking about the complexity of user interfaces, how it affects the acceptance of the software, and what should programmers do about it.

I'm not a UX specialist of any sort. But, I was a Gentoo user once. Gentoo is a Linux distribution that is famous for two things: 1) it is very flexible so every user can only build a part of the system they need, and 2) most installation/configuration operations are performed from your console via CLI tools (at best) or editing text files (at worst). I found out that long-time Gentoo users who are finally tired of it develop a picky taste for really good user interfaces. So I hope that my thoughts on that matter would be somewhat useful.

Why Do We Want The Interface Simple?

There is a cartoon that explains it all (like many other computing-related topics), which is linked in sidebar. Complex interfaces are annoying. They make people think, they make people actually fill endless forms, ask questions about it, satisfying the kafkaesque bureaucrat monster minds behind designing them. Remember all the "forms" you had to fill at consular sections, customs, and other public offices? They usually come with an instruction how to fill them twice as large... Well, the complex interfaces of computer software are even worse because they change as you interact with them!

Of course, most things you fill into these forms is necessary. Compared to Google search bar, which is approaching just answering a question you put there, they seem like getting to 20th floor by stairs compared to 2nd. But (provided the system cares about the citizens), these government guys really need that information you're to fill in into each form. Being long doesn't mean being complex, and a long-ish questionnaire really makes the user think less than a freetext field to enter your essay.

Bad Interface as a Programmer's Failure

So there is a huge class of problems where a complex, comprehensive interface is the answer. At the same time, there are complexities of other sort, which do not have any right to exist, and should be perished from each and every product by all means possible. It is when we make the user do our job, to follow an algorithm. Making machines follow algorithms is our job as programmers. We are paid for it, respected for it, and despised because of our devotion to it, but it's what we are to do. Note the emphasis on the word "we". We, not our users.

If you have to instruct your user like this, "if this checkbox is active, then you should set this flag; otherwise, set that flag", or "when you select this option, click the button below as well," then you are implementing a monster your users are going to hate. An only excuse to putting such decision is that you should build the tool immediately, and are going to improve it ASAP.

Not your job, actually? There are designer guys, User eXperience managers who should think this through rather than you? But do they really have a foundation that allows them enough variation? Don't they have to lower their expectations of what they can design because some of their ideas would require too costly architectural changes? I'm sure you at some point had a talk like, "Whoa, we can't implement this! It would require too much something!" Well, what it sometimes actually requires is additional effort on our part. We can--and do--affect whether the software is hard to use and has a handy interface, and you should be aware of that power in your hands from the very beginning. It's easy to screw up, and put too much limitations, and then ditch all interface improvements because their cost will rise.

Smells

Some designs are definitely programmers' failures. Look what I saw trying to transfer funds from one account to another in my online banking:

What's so damn hard in telling me when my transaction is going to complete if I perform it NOW? Doesn't the web server have access to clock??? Especially if it refers to a standardized time, but it could look up my local time via Javascript either. Why is it making *me* to look at my watch, and compute the date my transaction will complete? I know how programmers in banks are paid, don't tell me they aren't qualified to do this. It's just a lack of understanding that interface is bad if the user has to follow some kind of program rather than have a computer do it..

In my opinion, there are two smells that denote that your interface is wrong. It's badly designed if

1. you write policies and instructions instead of preventing mistakes programmatically. The designers of industrial machines got this ages ago. In addition to writing in big red letters DO NOT PUT YOUR HANDS HERE, they just install a damper that prevents you from doing this. This has been saving lives and limbs for centuries;
2. the interface can have a large number of inconsistent states. When you act upon a control, something changes in the interface, i.e. the interface's state changes. If your interface allows that in a comparatively large number of cases a state is inconsistent with your policy or your intention, or is just meaningless, it starts to smell. The fewer meaningless states you have, the better your interface is.

The reverse doesn't hold. If all states are meaningful, it doesn't mean that interface is already easy enough. It may lack handiness, expose too many parameters, greet users with insane default values. However, if it's too easy to make the wrong choice, the interface is definitely awful.

Game designers got it recently, and modern games highlight action items for you, expose less options where to go, and always provide an infinite box of ammo if you are to shoot your way through. The result? I see advertisements of Borderlands 2 on a bus stop. Gaming is no longer for nerds only!

Another case is automating the processes user shod not understand. One of these cases is installing drivers. Most of the time you install Linux, you have to install a proprietary driver for hour video card, and all the manuals say you should select the correct one based on its make. These manuals even provide you with instructions how to learn which video card is installed.

Why in the world can't the software look this up, and choose the correct video card on their own? New hardware comes out, and you can't know the names beforehand? Well, do guess! You think that casual users are smarter than your gueses? You update the wiki pages with instructions, why not update the software at the same time? No reason.

Back to game developers, they all bundle the latest version of DirectX, and automatically install it along with tge game itself without any, unnecessary questions asked from the user. Assassin's Creed 3 on billboards all over the city; that's the result.

How Easy Should the Interface Be?

Note that I didn't say anything about complexity; why? Some people think that the complexities of interface is what prevents others from using a product. This is an easy explanation. Many dream about a "brain-machine interface" as it would solve all problems with the complex interfaces. Myriads of buttons, overwhelming amount of gauges and interactive controls, and warnings like "your signature must fit completely in the box" will be useless because the answers to the questions would be transferred directly from human brain.

Contrary, the brain-machine interface is going to solve nothing. Because most users just do not have any brain.

The brain-machine interface does not jump over a barrier unachievable by other means. It is a result of gradual convergence of the means of control and our thoughts. The simplification of interfaces we see nowadays merely exposes the truth we should have unveiled years ago: if our thoughts are a mess, then a simpler interface doesn't solve anything. The interfaces are getting more and more simple, and people's persistent incapability to cope with them frightens me. I mean, are we really that dumb?

Since the user is going to be the problem, there's just one thing to do. To increase its knowledge. Extended to many systems, it could be called as increasing the likelihood that a person who encounters a system will infer the principles behind it, and starts asking the right questions.

One of the things that surprised me when I tried to deploy a wiki software in an office was that people couldn't create a page. I'm not sure if it was just an excuse to dodge a mundane job, but users reported that they couldn't find a button "Create New Page". Mediawiki, which is the software behind Wikipedia doesn't indeed has this button. Why? Because, unlike Google Docs, wiki is a set of interconnected pages, so pages not linked from elsewhere don't make sense. So the correct way to create a page is use it as if it's already exists, put a link to it. That simple and tricky at the same time.

What I think my failure was is that I didn't show how to use the wiki pages, didn't educate users. Without cross-reference, wiki pages are inferior to Google documents, which puts the whole idea into jeopardy.

No matter how simple your interface is, it is never going to be less complex than the concept behind the software. Search engine and other information-retrieval system are lucky: their concept converges to a single line of text (or a verbal query) where user enter what they need to know. Such systems then automatically suggest if user was looking for videos, images, and/or nearby shops (like Google currently does). However, when the concepts of information behind the scenes become more complex, such as maintaining a set of interconnected pages (wiki), or adjusting privacy settings (Google Plus).

So What?

So here's the list of things I would keep in mind as a programmer to make the interface of the product better:

Code With User Experience in Mind

Consult UX specialists early and often. Make sure your coding decisions you made at earlier stages of development do not prevent improving user experience after you get alpha-version feedback. The attitude "let's get it working first, and then think about User Experience," can easily lead to inability to actually improve it. It will be very easy not just to say, but to show with compelling evidence that you can't improve your interface because your code doesn't allow that. But really, putting code in front of User Experience is like putting the cart before the horse.

Convenient interface (or, let's say A Better User Experience) doesn't only mean that your knobs should be shiny. For instance, Google is famous for the speed of its products. Apple's interfaces (Mac, iPhone) are faster than many other their competitors (modern powerful Android phones changed it though). And it's not just convenience: being slow may even kill your project, as, I think, it killed one of mine.

And isn't it the most straightforward task for programmers: to make the gears faster?

Provide Early Response for User Input

If your user has to follow the rules when filing something, provide feedback ASAP. Don't make user click "Next" and only then receive response. Don't punish users for providing incorrect input because you think they should have read about the exact format for entering their SSN. Such approach is abomination. Do you really want your product make the same impression as an embassy where you apply for a visa or a public office full of nine-to-five clerks with their "read 10 pages of how to submit an application, and we'll reject it without explanation if something is wrong"? No, you don't.

That's why you provide pop-up hints, color input fields red until user gets it right. Just take a look how New Google Account window hints you and checks your input as you type, even before you reach the "Submit" button:

Decouple Rules From Code, Make Them Configurable

If your user should follow some rules (mainly when providing input to forms), try to make them re-configurable in a declarative style. This is important since the rules tend to change over time, though, I wouldn't say it's crucial. It's hard to get, too, especially since the previous section suggests that you should tailor your feedback instead of just verifying your model. Just make sure it doesn't end like this:

Credit card validation is my pet peeve... Why can't you tell me, "Sir, you missed a digit?" You know exactly how many digits there should be. But instead you're telling me something I can interpret as, "Your credit card is blocked!" This one, at least, doesn't ask me explicitly if I have a Visa or Master card, because you can learn it from the number I enter. Good girl.

Apparently, form validator they employed for that checkout page made it so hard to configure nice just-in-time validations that they resorted to the abomination of "error messages for the form". Of course, that's an additional challenge: to make this configuration just flexible enough for your purpose (, and here's where your judgement, as of a professional, comes to play. I thing that flexibility is one of the reasons "cancan" wins over "declaratice_auithorization" in Ruby on Rails web authorization plugins: the former is much more flexible and easier to configure.

Educate Your Users

If the concept your software tries to manage is complex, then simplifying the interface will only increase frustration because user will feel like he doesn't have sufficient tools to tailor the information to its needs. Instead, invest time into making users more informed. Make educational, not promotional videos; Talk at conferences, explain the concepts as soon as users encounter difficulties automatically by popping out videos. The thing is that, even if your interface is not ideal yet, it will never become simpler than those concepts, so it will never hurt to explain them. You can also pop up a chats with customer representative. The latter was recently employed by many service providers, and now their websites pop up windows offering human help if you are lost while browsing the site.

You think it's a job of your PR manager, not yours? Well, are you sure your PR folks understand the concepts in the first place?

Conclusion

I tried to summarize my thoughts on what makes a good user interface, why the simple interface isn't necessarily the best, and what to do about it as a programer. And you really can do a lot to improve the interface of your software: devise the ways of automating figuring out unnecessary details (such as video card make) for your users, improve speed, explain the concepts behind and typical use-cases. And, as a programmer, your unwillingness to deal with this can destroy your project, well, just as many other things you fail to take care of can.

Wikipedia used to do a pretty bad job at explaining the theoretical foundations behing the different consistency models of multithreaded/distributed systems. Especially cryptic was the definition of "quiescent consistency", which I try to explan further in this post. Just take a look at the articles, and see how inconsistent the consistency model descriptions are. I'll try to get them together.

What is a Consistency Model?

When one describes how a distributed system behaves, one typically mentions a "consistency model". This "model" describes the difference in behavior between a system in a single-threaded operation and a multi-threaded or a multi-machine operation of a system.

Assume that you're implementing a data structure (a set, for instance; say, you can add/remove elements, and check for presence). The specification (model) for its behavior usually implies that the operations are performed sequentially. For instance, a set indicates a presence of an element if ant only if it was added before the presence check, and not removed after that. The terms "before" and "after" imply that there is an order in operations over that structure. While it is straightforward to know the order of operations in a single thread, it gets unclear if there are several threads or machines:

• Calls may overlap. If two threads call methods on the same structure at approximately the same time, the calls may overlap because they don't happen simultaneously in real world. In what order the calls took effect is not clear, however, because thread scheduling or network connection introduces arbitrary delays in processing.
• Calls may not take effect immediately. When a method call returns, it is sometimes not clear when the operation actually "takes effect." By adjusting what "taking effect" means, the programmer may increase the speed of some operations at the expense of their immediacy or strictness guarantees. For example, a stack data structure might fail to preserve the order of the elements inserted in order to make the insertions faster. This might make sense because the "ordering" of events observed in different parts of a distributed system is not that well-defined to begin with. I talked about why this is natural in my other post "Relativity of Simultaneity in Distributed Computing".

Object-Oriented Model and Executions

A consistency model usually assumes Object-Oriented approach to describing a system. Assume that we have something (say, a set), and its internal state can be observed and altered only through a specific set of methods (say, add(elem), remove(elem), and bool in(elem)). The OO approach assumes that internal state is concealed or unknown, so we do not define consistency models in terms of object's state. Instead, we place restrictions on the values these methods may return based on when other methods were called in different threads or machines.

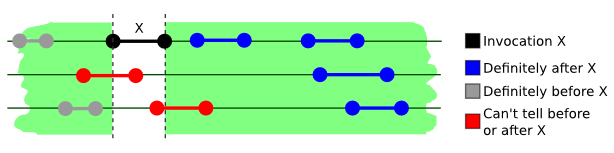
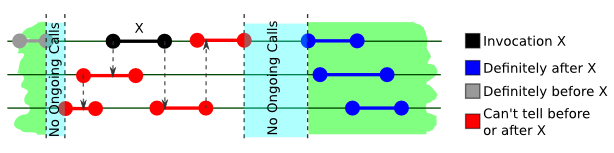
In practice, method calls don't happen instantly, and the model acknowledge this. The methods called, with start and finish times, their arguments, and their return values is referred to as an execution. An execution is usually depicted as intervals plotted onto lines. The parallel horizontal lines represent the simultaneous passing of common, global time in different threads (ignoring for now, if this concept of global passing of time is valid). The intervals are the method calls, their beginning corresponding to the time the method was called and the end when the method returned. The call arguments and the return values as well as the method and object name are usually written near the method call. Here's a sample execution of a set object:

We will omit the actual call values further because consistency models do not operate in terms of actual arguments and values, but rather try to "map" concurrent executions to sequential ones. In our further diagrams we will also assume that all methods are called against the same object.

Since consistency model imposes restrictions on an execution, the latter may match or not match a consistency model. A data structure adheres to a consistency model iff every execution over its methods we may observe adheres to it. That's what's hidden behind such phrases as "sequentially consistent stack".

No Consistency

The most important consistency "model", is, of course, no consistency. Nothing is guaranteed. The methods called on the object may observe anything. We may add two different elements to an empty set, and observe that the size of set is three, and none of these elements is what we added.

All other consistency models are opposite to the No Consistency in the following sense. They all assume that the method calls may be re-arranged in a single-threaded sequence that is correct with respect to the object's specification. Let's call it arranged correctly in the rest of the post. For example, a set of pets that adheres to any consistency model described below can't tell us that it contains a cow, if only dogs were added to it.

"Multithreading" Consistency Models

What I discovered is that consistency models are divided into two categories: that lean to multithreading (shared memory multiprocessor systems), and to "multi-machine" (distributed systems). I find the former category more formal and mathematical; these models can be used to describe behavior precise enough to allow math-level, rock-solid reasoning about system properties. Some "distributed" consistency models are less precise in their definition, but are widely mentioned in documentation and description, and do allow users to make informed decisions.

Let's start with the "multithreading" ones.

Strong Consistency aka Linearizability

This is the most important consistency model to understand.

An execution is strongly consistent (linearizable) if the method calls can be correctly arranged in a sequence that retains the order of calls that do not overlap in time no matter which thread calls them. (See "No Consistency" section for definition of "correctly arranged").

In other words, if two calls overlap, then they may "take effect" in any order, but if a call returns, then you may be sure it already worked.

A more anecdotal definition is "before the method returns, it completely takes effect consistently with other threads." This is also usually called "thread safety" unless more precise definition of consistency model is specified. This is quite a stringent restriction, especially for distributed systems, where threads run on different machines.

While it's unclear if the method calls marked in red happen before or after X, an important property must also hold. There must exist a sequence of calls such that they all make sense as if they were called from one thread, while still satisfying the ordering constraint described above holds.

Two linearizable executions combined also form a linearizable execution. This is an important property, since it allows us to combine linearizable components to get strongly consistent systems. This is not true for other models, for instance....

Sequential Consistency

An execution is sequentially consistent if the method calls can be correctly arranged in a sequence that retains the order of method calls within each thread.

The calls in different threads can be re-arranged arbitrarily, regardless of when they start and when they end in relation to other calls.

An example of a sequentially consistent system is a naive notion of RAM in multi-core processor. When different threads read from the memory, they actually read from a cache or a register, which is synchronized with a common RAM at writes. While values read and written on different cores may not be immediately synchronized (cores may diverge in the notion of what value a cell contains), the values read and written on the same core are always consistent with each other. This is naive, though: even this guarantee is relaxed by modern compilers, and accesses to different variables within one thread can be reordered (as far as I recall, ARM platforms are guilty of this).

You might notice that the definition of sequential consistency does not directly prevents methods to return values from the future (i.e. to read what will be written later in a different thread). Yet I claim that RAM is sequentially consistent; how's that? The thing is that each execution should be sequentially consistent. If read and write do not overlap, and write follows the read, we may just stop the program between them. Since each execution should be consistent, the value read should be written before in some thread. Therefore, this "future prediction" is not possible in consistent data structures (not only those that are "sequentially" consistent) even that the definition doesn't directly prevent it.

However, if we combine two sequentially consistent executions, the result won't be sequentially consistent. But there is another model, weaker than linearizability, that makes it possible.

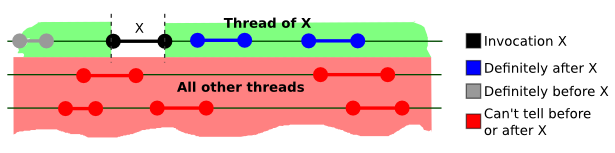
Quiescent Consistency

An execution is quiescently consistent if the method calls can be correctly arranged in a sequence that retains the order of the calls separated by quiescence (a period of time when no method is running in any thread).

This consistency condition is stronger than sequential consistency, but is still not strong enough to be widely adopted as a discriminator. Implementations exist, e.g. see my other post for a more in-depth example of a quiescently consistent stack. The model is mostly used is to attain a higher degree of concurrency than linearizable components allow.

Quiescent consistency is rarely employed in production systems. Here's an example of how one can implement a quiescently consistent system: assume that all writes are cached, and the cache is flushed to a persistent storage when there are no ongoing writes (or after it reaches certain size). More specialized data structures that are quiescently consistent exist.

However, many high-load distributed systems are almost never quiescent. A typical distributed web service may consist of hundreds of caches, frontends, and backend instances. If the service is really high-load (say, serves order of millions of requests per seconds), no component is quiescent ever. Systems that rely on quiescence to work (e.g. written in garbage-collected languages) have to "trigger quiescence" (this happens when some Java virtual machines trigger "heap compaction"), which slows the system down. Then, one has to employ tricks to improve their tail latency.

Quiescent consistency components can be combined to form quiescently consistent components again. Note also, that strong consistency implies quiescent consistency, hence you can combine these two kinds of systems, and the result will be quiescently consistent.

"Distributed" Consistency Models

The following models are usually seen in the context of distributed systems, i.e. those that reside on multiple machines, communication between which is slow enough. To bring Object-Oriented abstraction to distributed systems, programmers invented "Remote Procedure Call" (RPC) pattern. Method calls (object identifiers, method name, and arguments) are encoded into messages that are then sent across the network to specified destination, which may be the part of the encoding too. Method calls that do not expect a reply (say, unreliable "fire-and-forget" writes) may be treated as instantaneous.

Eventual Consistency

A system is eventually consistent if the method calls can be correctly arranged in a sequence that retains the mutual order of calls separated by a sufficiently long period of time. The "sufficiently long period of time" is system-specific.

Usually, eventual consistency is combined with sequential consistency, in a stanza like: "the data written to the database is immediately visible from the same process and eventually visible from other [concurrent] processes".

The eventual consistency definition—as well as its understanding—is intentinally vague on how much time it would take, and whether this time depends on the call history. We can't really tell how soon an eventually consistent set will respond that an element X exists in it after it was added. But "eventually" it will.

This looks quite useless from a mathematical perspective since the loose definition doesn't help draw conclusions. What is it used for then? Well, users usually expect strong consistency from a system, and if it is different, it needs to be pointed out. Eventual consistency is actually a limitation of liability; it's used to convey that the system can't guarantee that different threads become in sync immediately. However, the system is engineered in such a way that they eventually take effect. Here's an example (here's more on eventual vs. strong consistency)

Some authors, according to wikipedia, require that no method calls should be invoked during the "long period of time" for system to get in sync. This actually sounds like a stronger version of quiescent consistency, where a qualifying quiescence should be long enough.

Strict Consistency

An execution is strictly consistent if the method calls sorted by completion time are correctly ordered.

This is as simple and powerful as it's impossible to attain in most practical systems that have more than one thread. First, it order calls according to "global" time, which is a purely mathematical abstraction unachievable in real life, both according to Physics, and to the theory of distributed computing. Second, any implementation I might imagine would essentially disallow multithreading per se.

This is my rendition on the more "official" definition (1, 2), which defines a strictly consistent system as one where any read operation over a certain item returns the value supplied to the latest write operation according to global time counter. I don't like this definition because it needs to distinguish between "reads" and "writes", and introduces the concept of "data item"—i.e. it breaches the object-oriented approach. Still, I'm sure that if the system really consists of "data items," the definition at the beginning of the section would work as well.

Serializability

An execution is serializable if its methods in each thread are grouped in contiguous, non-overlapping transactions, and the methods can be correctly ordered in such a way that transactions are still contiguous.

In other words, the outcome of a sequence of method calls can be described as a serial execution of transactions, where methods of different transactions are not mingled, while the transactions actually overlap in time across different threads. The useful outcome here is that calls within overlapping transactions can be reordered, even if they don't overlap. However, "serializability" is not enough to describe the system: while it limits reordering of methods across transactions, it is unclear to what extent transactions can be reordered themselves. This is a job for a different consistency model. And serializability is usually used to "remind" about this important property of transaction-based systems.

Practice

Some systems provide several levels of consistency for operations (like the App Engine's High-Reliability Datastore linked above). You should understand what tradeoffs each model has to make the decision best suitable for your specific application.

Most system you encounter will be not consistent at all ("thread-unsafe"), or linearizable (this is what usually understood by "thread-safe"). If the consistency model differs, it will be noted explicitly.

Strictly speaking, most systems that claim linearizability will be not consistent due to bugs, but these nasty little creatures aren't suitable for careful scientific discourse anyway.

Now that you know what consistency models are out there (and that they actually exist), you can make informed decisions based on what's specified in documentation. If you're a system developer, you should note that you are not bound to choose between linearizability and "thread-unsafety" when designing a library. The models presented above may be viewed as patterns that enumerate what behaviors in multithreaded context are considered universally useful. Just consider carefully what your users need, and do not forget to specify which model your system follows. It will also help to link to something that explains what lies behind the words "somethingly consistent" well--like this post, for instance.

Comments imported from the old website

Hooray! The Airbus finally brought me to the land where law is taken slightly more seriously than in Russia. With great responsibility, however, usually comes great power, and a lot of absolutely legal video streaming services are available in the U.S. Moreover, my corporate-sponsored temporary apartment has a large, like, 30-inch TV, and it would be a sin to just let it collect dust in silence.

No, I couldn't just watch cable TV! The very idea that I watch something on a predefined schedule is not appealing to me. I'd have to spend money on a TiVo or something that records TV shows anyway. And what about DVDs and feature movies? TV shows isn't the only thing I watch, by the way. And what about shows that are not airing? how to watch older seasons? No, TV is for the weak.

Streaming has even some advantages compared to these filthy, illegal torrents. You can start watching an HD movie at once, rather than wait until its download is complete!

So the most rational idea is to stream movies from Internet via my desktop PC to the TV. Surprisingly, the hard thing was that I use Linux, and this was far from the usual "OMG settings are so complex in Lunupz, I can't do console!" whining.

"Nobody uses Linux... Get a real OS, nerds."

The first thing to choose is the content provider. And that's where Linux users get into the ambush.

The thing is that the mission statement of GNU contradicts what content vendors are trying to achieve. Linux, or, more specifically, "GNU/Linux", because we're talking about operating system rather than the kernel here, is all about being open, allowing user to see what software is running and have full access to its contents. Content providers, however, insist that DRM—one of technologies to revoke control over content—is imposed onto end-users. This is why it is not easy to find Linux support in these matters.

Netflix

The first service to try was Netflix. Actually, that million of dollars worked well: I only heard about Netflix form a Communications of the ACM article (as far as I recall it was this one) about the Netflix prize. No wonder I decided to try it first.

When I came to the U.S., I didn't have any personal computer at all. In Russia, we have an adage, "to come to Tula with one's own samovar". Tula was famous for its samovar-makers, and the adage mocks those who carry the specific items they possess to places that naturally have a great choice of such items. So no wonder I didn't bring my, like, 15-pound chassis here. Instead, I bought a 4-core i8 from Best Buy, but for the several first days all I had was Galaxy Note smartphone/tablet. Netflix installed smoothly from Google Play, I watched some TV shows there, and I thought I won't have any problems at my desktop PC.

I was very wrong. Netflix doesn't have a way to run under generic Linux distribution. Windows7, MAC—you go, Android—here you are, GNU/Linux—go fsck yourself. Seemingly reassuring was that it ran under ChromeOS, but that was only for proprietary Google's Chromebooks. Yes, even the new Samsung $250 ARM Chromebook. Recently, Google and Netflix managed to arrange a seamless delivery of video to the laptops, while it didn't work until the March'13. I tried it on mine, and it works! However, if you install ChromiumOS in a virtual machine, it also won't work (I tried.) A Netflix Chromium plugin also looked promising, but it's just a frontend to their web-site, and doesn't offer the playback capabilities to Chromium itself; there are a lot of angry reviews by Linux users, and a response to them is a caption to this section.) Here's a blog post with a more comprehensive overview.

Hulu

Hulu, on the contrary, has a GNU/Linux application. However, very few of their movies were available in HD, and I was not interested in those that were. So I had to skip this service.

Amazon

Yes, Amazon has a movie service as well. Marketing also worked here: I learned about this from IMDb, which was bought by Amazon years ago. And Amazon is the thing that finally worked but not without a plot twist.

The thing is that Amazon doesn't support GNU/Linux PCs for its HD movie content! Yep, that's right, check their list of compatible devices. You see a list of TiVo-s, Consoles, Smart TVs, and an iPad, but where's the PC? Nope, it's not there. Yet it works.

That's right, when you pay for streaming an HD TV show, it just plays in your browser. It requires Flash, though. The list of compatible devices apparently means that if you "buy" a movie instead of renting it, you can only download it to one of the compatible devices rather than to your PC.

I used to think that it was a mistake of sorts, but the further research revealed that Amazon would probably love to stream all sorts of HD stuff to as wide variety of users as possible. This looks like a matter of what publishers allowed Amazon to do. They seemingly allow HD movies to tivoized and DRM-ready devices, and just don't care that much about TV shows. Streaming the movies I tried didn't work.

Equipment

To connect a TV to your PC, you'll need some extra equipment. When I looked at the price of 25-feet HDMI cable at BestBuy, I was shocked: it cost more than my monitor! So I bought that 25-cable from Amazon for $14. You should already have Ethernet cable, but in case you don't you may buy it there as well, and, of course, you should have a good and fast connection.

Setting up Linux

The screenshots below are from the Linux distro that I use at home, namely ROSA Marathon 2012.

First, I connected the TV via cable, turned it on, and set the input to the corresponding slot. I'm not sure if it's necessary, but if never hurts to do this first.

Unfortunately, KDE settings (available via "Configure Your Desktop" → "Display and Monitor") thought that I don't have any other monitors:

It remained this way even after I managed to configure it, so don't rely on it that much.

The second thing to try was the settings for my video card, nVidia GeForce GT 520. That's where I finally found managed to do this. This configuration tool will need to write to your /etc/X11/xorg.conf file, so make a backup first by copying it somewhere. Because of this very thing, you should run it under root (sudo won't work, use its KDE-specific counterpart):

$ kdesu nvidia-settings

Got to "X server Display Configuration" tab, and press "Detect Displays." Your connected TV should appear there. You could try TwinView, but you don't want to spread your desktop across two screens (it makes no sense), and TwinView sometimes limits your bigger monitor resolution to your TV resolution, which you don't want. However, TwinView doesn't require restarting X.

So you could try TwinView, and resort to "Separate X screens" if TwinView doesn't work. If the "Separate X screens" option is not shown, don't panic, select it, and other options should become available (it's a bug); maybe, you'll have to Quit with saving configuration, and reopen again. The goal is to set the "Configuration" to "Separate X screen (requires X restart)" for both displays:

I also found out that the least intrusive is to place the TV display "Below" the main one. This means that the mouse will appear on the TV screen when you move it over the bottom edge.

Click "Save to X configuration File" (if you get an error here, you forgot to run as root with kdesu), and Quit. Restart your X server (or restart your PC), and there you go.

Now we should actually run something on that new screen. It's not that easy. There are different displays that are different X processes, and within one process live several "screens," which we have set up.

Remember, that videos play from your browser? So you should start a web browser on that another screen (this is not required if you use TwinView - just drag browser window to where your TV screen resides). Screens are set up nearly like displays, via the DISPLAY variable; the screen number follows the display number after a dot. I didn't manage to start a second Firefox window on that screen, unfortunately. But nowadays we do have a choice.

$ DISPLAY=:0.1 chromium-browser amazon.com
$ DISPLAY=:0.1 firefox amazon.com

Now move your mouse beyond of the bottom edge of the screen, and start the movie you like. Pro tip: start browser as usual, log in to it, and only then re-start it on another screen to avoid excessive strain on your neck.

Start the movie... wait-wait-wait, why is the sound going from my PC speakers rather than from the TV itself?? Back to configuration. Open KDE desktop configuration tool, click on "Multimedia", select Phonon, and adjust the priority of the "Audio Playback" (not of any of subcategories, but of the category itself).

As usual with the sound, adjust mixer settings of HDMI device. Use alsamixer console command and unmute/volume-up everything there like crazy if the usual mixer doesn't give results:

For me, sometimes, I had also to select another profile on "Audio Hardware Setup" tab. Now you're set. The sound should be re-routed to TV without restarting the browser, but, again, give it a try if it doesn't work.

Enjoy. Here's a proof that it works:

Internet connection is not used very intensively, and I'd be able to watch, like, three HD videos simultaneously:

That's how you fight your way through bugs, tricky settings, "X displays" (wtf? why do I need to worry about that?) Of course anybody would love to avoid all that. But that's basically the same thing that you have to select and tune things like medical insurance on your own, because you are, as with Linux, in the land of the free.